Main Navigation Links
Objectives
The Show Me Your Receipts project is designed to:
(1.) Meet one of the learning objectives of the VCCS (Virginia Community College System) standards for:
MTH 132: Business
Mathematics
(Provides instruction, review, and drill in percentage, cash and trade discounts, mark-up,
payroll, sales, property and other taxes, simple and compound interest, bank discounts, loans,
investments, and annuities).
MTH
133: Mathematics for Health Professions
(Presents in context the arithmetic of fractions and decimals, the metric system and dimensional
analysis, percents, ratio and proportion, linear equations, topics in statistics, topics in
geometry, logarithms, topics in health professions including dosages, dilutions and IV flow rates.).
MTH 154:
Quantitative Reasoning
[Solve real-life problems requiring interpretation and comparison of various representations of
ratios (i.e., fractions, decimals, rates, and percentages including part to part and part to
whole, per capita data, growth and decay via absolute and relative change)].
(2.) Meet the QM (Quality Matters) and USDOE (United States Department of Education) requirements for
distance education as regards the
provision of RSI (Regular and Substantive Interaction).
Federal Register: Distance Education and Innovation
St. John's University: New Federal Requirements for Distance Education: Regular and
Substantive Interaction (RSI)
Student – Content Interaction: Very high
Student – Student Interaction: Flexible
Student – Faculty Interaction: Flexible
(3.) Solve applied problems involving percents.
Example Guides
Case 0: What Item?
SamDom4Peace did not pay a sales tax in one of the items.
Identify the item.

This is the receipt:

Let:
SM ORNGE BA = Item 1
ENH SERIES = Item 1
There are two items but only 1 tax rate of 1%
Let us find the tax amount of 1% tax for each item
$ 1\% = \dfrac{1}{100} = 0.01 \\[5ex] \underline{Item\;1} \\[3ex] Cost = 4.98 \\[3ex] Tax = 0.01(4.98) \\[3ex] = 0.0498 \\[3ex] \approx \$0.05 \\[5ex] \underline{Item\;2} \\[3ex] Cost = 5.47 \\[3ex] Tax = 0.01(5.47) \\[3ex] = 0.0547 \\[3ex] \approx \$0.05 \\[3ex] $ As we can see, the tax amount is approximately the same for both items.
So, how can we figure out the item?
Note the responses of your students.
Advise them accordingly.
Case 1: Given: Initial price and Tax rate
Calculate:
(a.) Tax
(b.) Total price

This is the receipt:

Let:
EL 6PK REPE = Item
$ (a.) \\[3ex] 10\% = \dfrac{10}{100} = 0.1 \\[5ex] \underline{Item} \\[3ex] Cost = 23.96 \\[3ex] Tax = 0.1(23.96) \\[3ex] = 2.396 \\[3ex] \approx \$2.40 \\[3ex] (b.) \\[3ex] Total\;\;price = 23.96 + 2.396 \\[3ex] = 26.356 \\[3ex] \approx \$26.36 $
Case 2: Given: Tax rate and Total price
Calculate:
(a.) Initial price (Subtotal)
(b.) Tax

This is the receipt:

Let the subtotal (sum of the initial prices) of the items = p
$ (a.) \\[3ex] 5.3\% = \dfrac{5.3}{100} = 0.053 \\[5ex] \underline{Item} \\[3ex] Subtotal = p \\[3ex] Tax = 0.053(p) = 0.053p \\[3ex] Total\;\;price = p + 0.053p \\[3ex] = 1.053p...Calculated \\[3ex] = 34.64 ...Given \\[3ex] \implies \\[3ex] 1.053p = 34.64 \\[3ex] p = \dfrac{34.64}{1.053} \\[5ex] p = 32.89648623 \\[3ex] Subtotal \approx \$32.90 \\[3ex] (b.) \\[3ex] Tax = 0.053(32.89648623) = 1.74351377 \\[3ex] Tax \approx \$1.74 $
Case 3: Given: Tax rate and Tax (Use $1.29638)
Calculate:
(a.) Initial price (Subtotal)
(b.) Total price

This is the receipt:

Let the subtotal (sum of the initial prices) of the items = p
$ (a.) \\[3ex] 5.3\% = \dfrac{5.3}{100} = 0.053 \\[5ex] \underline{Item} \\[3ex] Subtotal = p \\[3ex] Tax = 0.053(p) = 0.053p...Calculate \\[3ex] Tax = 1.29638 ... Given \\[3ex] \implies \\[3ex] 0.053p = 1.29638 \\[3ex] p = \dfrac{1.29638}{0.053} \\[5ex] p = 24.46 \\[3ex] Subtotal \approx \$24.46 \\[3ex] (b.) \\[3ex] Total\;\;price = 24.46 + 1.29638 \\[3ex] = 25.75638 \\[3ex] \approx \$25.76 $
Case 4: Given: Five items, Part of the subtotal (Initial prices of four items),
Tax rate, and Total price
Calculate:
(a.) Subtotal (sum of the initial prices)
(b.) Tax
(c.) Initial price of the fifth item
(d.) Unit price of the fifth item per pound

This is the receipt:

Let the subtotal (sum of the initial prices) of the items = p
$ (a.) \\[3ex] 1\% = \dfrac{1}{100} = 0.01 \\[5ex] \underline{Item} \\[3ex] Subtotal = p \\[3ex] Tax = 0.01(p) = 0.01p \\[3ex] Total\;\;price = p + 0.01p \\[3ex] = 1.01p...Calculated \\[3ex] = 23.03 ...Given \\[3ex] \implies \\[3ex] 1.01p = 23.03 \\[3ex] p = \dfrac{23.03}{1.01} \\[5ex] p = 22.8019802 \\[3ex] Subtotal \approx \$22.80 \\[3ex] (b.) \\[3ex] Tax = 0.01(22.8019802) = 0.228019802 \\[3ex] Tax \approx \$0.23 \\[3ex] (c.) \\[3ex] \underline{Four\;\;items} \\[3ex] Initial\;\;price = 4.98(4) = \$19.92 \\[3ex] \underline{Five\;\;items} \\[3ex] Subtotal = \$22.8019802 \\[3ex] Initial\;\;price\;\;of\;\;5th\;\;item \\[3ex] = 22.8019802 - 19.92 \\[3ex] = 2.8819802 \\[3ex] \approx \$2.88 \\[3ex] (d.) \\[3ex] Let\;\;unit\;\;price\;\;of\;\;5th\;\;item/pound = k \\[3ex] 4.96 * k = 2.8819802 \\[3ex] k = \dfrac{2.8819802}{4.96} \\[5ex] k = 0.5810443952 \\[3ex] Unit\;\;price \approx \$0.58 $
Case 5: Given: Tax, Sam's Club credit, Remaining balance (Use
$11.1798)
Calculate:
(a.) Total price
(b.) Initial price (Subtotal)
(c.) Tax rate

This is the receipt:

$ (a.) \\[3ex] Sam's\;\;club\;\;credit = \$4.96 \\[3ex] Remaining\;\;balance = \$11.1798 \\[3ex] Total\;\;price = 4.96 + 11.1798 \\[3ex] = 16.1398 \\[3ex] \approx \$16.14 \\[3ex] (b.) \\[3ex] Subtotal = Total\;\;price - Tax \\[3ex] = 16.1398 - 0.16 \\[3ex] = 15.9798 \\[3ex] \approx \$15.98 \\[3ex] (c.) \\[3ex] What\;\;\%\;\;of\;\;15.9798\;\;is\;\;0.16? \\[3ex] \underline{Percent-Proportion} \\[3ex] \dfrac{is}{of} = \dfrac{what\%}{100} \\[5ex] \dfrac{0.16}{15.9798} = \dfrac{what\%}{100} \\[5ex] what\% = \dfrac{0.16 * 100}{15.9798} \\[5ex] what\% = 1\% \\[3ex] Tax\;\;percent = 1\% $
Case 6: As at March 2024, the City of Harrisonburg in the State of Virginia charges 1%
sales tax on raw foods and fruits and a high tax rate
on cooked food.
(I guess they want Virginians to cook their meals.)
Chukwuemeka was hungry and decided to buy hot food at Walmart.
The hot food is high in calories and is a source of carbohydrates (carbs).
He also decided to buy a bag of fresh oranges to provide essential vitamins.
The receipt shows three tax rates: the tax rate on the oranges (shown) and two different tax
rates on the hot food (not shown).
Given:
(I.) Initial price of the bag of oranges
(II.) Initial price of the hot food
(III.) Tax rate on the bag of oranges
(IV.) Tax on the bag of oranges
(V.) 1st tax on the hot food (Use $0.39591)
(VI.) 2nd tax on the hot food (Use $0.5229)
Calculate:
(a.) Subtotal (Sum of the initial prices)
(b.) 1st tax rate on the hot food
(c.) 2nd tax rate on the hot food
(d.) Total price

This is the receipt:

$ (a.) \\[3ex] Subtotal = 4.98 + 7.47 \\[3ex] Subtotal = \$12.45 \\[3ex] (b.) \\[3ex] What\;\;\%\;\;of\;\;7.47\;\;is\;\;0.39591? \\[3ex] \underline{Percent-Proportion} \\[3ex] \dfrac{is}{of} = \dfrac{what\;\%}{100} \\[5ex] \dfrac{0.39591}{7.47} = \dfrac{what\;\%}{100} \\[5ex] what\;\% = \dfrac{0.39591 * 100}{7.47} \\[5ex] what\;\% = 5.3\% \\[3ex] 1st\;\;tax\;\;rate = 5.3\% \\[3ex] (c.) \\[3ex] What\;\;\%\;\;of\;\;7.47\;\;is\;\;0.5229? \\[3ex] \underline{Percent-Equation} \\[3ex] \dfrac{what}{100} * 7.47 = 0.5229 \\[5ex] what = \dfrac{0.5229 * 100}{7.47} \\[5ex] what = 7 \\[3ex] 2nd\;\;tax\;\;rate = 5.3\% \\[3ex] (d.) \\[3ex] Total\;\;price = 12.45 + 0.39591 + 0.05 + 0.5229 \\[3ex] = 13.41881 \\[3ex] \approx \$13.42 $
Case 7: Samuel placed two different online orders on two different days on the
Amazon website.
The two different orders were sent to the same address in the State of Virginia.
None of the orders has food or drinks.
However, the orders were charged different tax rates.
1st Order:
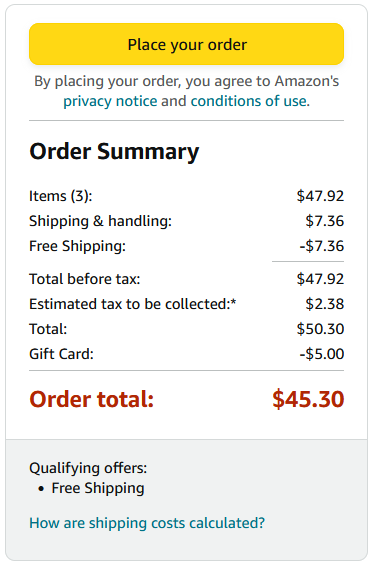
2nd Order:
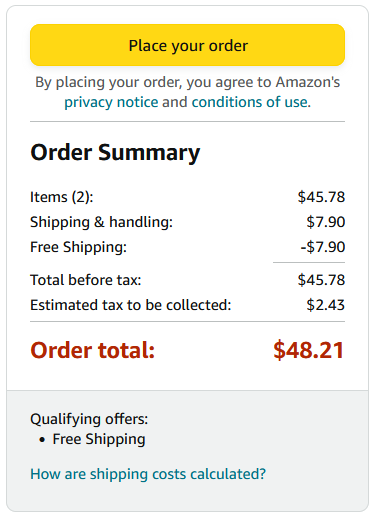
(a.) Calculate the tax rate for the 1st order.
(b.) Calculate the tax rate for the 2nd order.
(c.) Samuel asked you to explain why the tax rates were different.
(i.) Ask Samuel at least one question in that regard.
(ii.) Provide at least one explanation to Samuel.
Let the subtotal (sum of the initial prices) of the items = p
$ (a.) \\[3ex] \underline{1st\;\;Order} \\[3ex] What\;\;\%\;\;of\;\;47.92\;\;is\;\;2.38? \\[3ex] \underline{Percent-Equation} \\[3ex] \dfrac{what}{100} * 47.92 = 2.38 \\[5ex] what = \dfrac{2.38 * 100}{47.92} \\[5ex] what = 4.966611018 \\[3ex] Tax\;\;rate = 4.966611018\% \\[3ex] (b.) \\[3ex] \underline{2nd\;\;Order} \\[3ex] What\;\;\%\;\;of\;\;45.78\;\;is\;\;2.43? \\[3ex] \underline{Percent-Proportion} \\[3ex] \dfrac{is}{of} = \dfrac{what\;\%}{100} \\[5ex] \dfrac{2.43}{45.78} = \dfrac{what\;\%}{100} \\[5ex] what\;\% = \dfrac{2.43 * 100}{45.78} \\[5ex] what\;\% = 5.307994758\% \\[3ex] Tax\;\;rate = 5.307994758\% $
Case 8: Given:
(I.) Two items:
2nd item is 20LB GV HML
1st item is GE STRT JEA
Note the interchange here as opposed to the receipt
(II.) Subtotal of the two items
(III.) Different tax rates for the two items
(Tax 1 for the 1st item and Tax 2 for the 2nd item)
(IV.) Different taxes for the two items
(Use $0.84694 for the 1st item and $0.1674 for the 2nd item)
(V.) Total price
Calculate:
(a.) Initial price of the 1st item
(b.) Initial price of the 2nd item

This is the receipt:

Let the:
initial price of the 1st item = c
initial price of the 2nd item = d
$ \underline{Items} \\[3ex] Subtotal = \$32.72 \\[3ex] c + d = 32.72 ...eqn.(1) \\[5ex] \underline{Taxes} \\[3ex] Tax\;\;rate\;1 = 5.3\% = \dfrac{5.3}{100} = 0.053 \\[5ex] Tax\;\;rate\;2 = 1\% = \dfrac{1}{100} = 0.01 \\[5ex] Tax\;1 = \$0.84694 \\[3ex] Tax\;2 = \$0.1674 \\[3ex] Sum\;\;of\;\;taxes = 0.84694 + 0.1674 = 1.01434 \\[3ex] 0.053c + 0.01d = 1.01434...eqn.(2) \\[5ex] \underline{Elimination\;\;by\;\;Subtraction\;\;Method} \\[3ex] 100 * eqn.(2) \implies \\[3ex] 5.3c + d = 101.434...eqn.(3) \\[3ex] eqn.(3) - eqn.(1) \implies \\[3ex] (5.3c + d) - (c + d) = 101.434 - 32.72 \\[3ex] 5.3c + d - c - d = 68.714 \\[3ex] 4.3c = 68.714 \\[3ex] c = \dfrac{68.714}{4.3} \\[5ex] c = 15.98 \\[3ex] \underline{Substitution\;\;Method} \\[3ex] From\;\;eqn.(1) \\[3ex] d = 32.72 - c \\[3ex] d = 32.72 - 15.98 d = 16.74 \\[3ex] Initial\;\;price\;\;of\;\;the\;\;1st\;\;item = \$15.98 \\[3ex] Initial\;\;price\;\;of\;\;the\;\;2nd\;\;item = \$16.74 $
Case 9: Given:
(I.) Initial price
(II.) Discount
(III.) Percent Discount
(IV.) Sale price
But:
The percent discount on the label is an approximate value.
Calculate the exact percent discount.

We have several approaches to solve this question.
Use any approach you prefer.
$ Initial\;\;price = 2.70\;lb * \dfrac{\$8.98}{1\;lb} = \$24.246 \\[5ex] Sale\;\;price = 2.70\;lb * \dfrac{\$6.98}{1\;lb} = \$18.846 \\[5ex] \underline{Algebraic\;\;Thinking} \\[3ex] Let\;\;\%\;discount = p \\[3ex] p\% = \dfrac{p}{100} = 0.01p \\[5ex] Discount = p\%\;\;of\;\;24.246 \\[3ex] = 0.01p(24.246) \\[3ex] = 0.24246p \\[3ex] Sale\;\;price = p\%\;\;off\;\;24.246 \\[3ex] = 24.246 - 0.24246p \\[3ex] \implies \\[3ex] 24.246 - 0.24246p = 18.846 \\[3ex] 24.246 - 18.846 = 0.24246p \\[3ex] 0.24246p = 5.4 \\[3ex] p = \dfrac{5.4}{0.24246} \\[5ex] p = 22.27171492 \\[3ex] \therefore \%\;discount = 22.27171492\% \\[5ex] \underline{Percent-Proportion} \\[3ex] What\;\;\%\;\;of\;\;24.246\;\;is\;\;18.846? \\[3ex] \dfrac{is}{of} = \dfrac{what\;\%}{100} \\[5ex] \dfrac{18.846}{24.246} = \dfrac{what\;\%}{100} \\[5ex] what\;\% = \dfrac{18.846 * 100}{24.246} \\[5ex] what\;\% = 77.72828508\% \\[3ex] \%\;discount = 100\% - 77.72828508\% \\[3ex] \%\;discount = 22.27171492\% $
Project Requirements
(1.) Independent Study: This is an individual project.
You may collaborate with another student. However, it is an individual project.
It is not a group project.
(2.) The image of every receipt you use must be clear, sharp, and taken on a good background.
Please use the Insert → Pictures icon to insert the image directly.
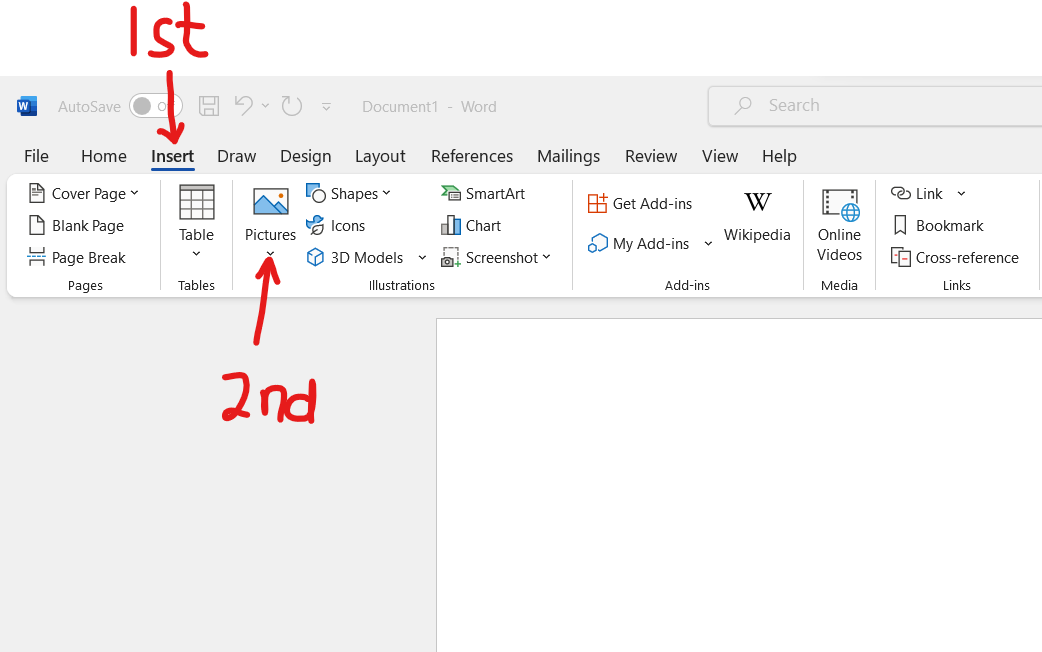
(3.) Critical Thinking: I did 10 different cases as seen in the Example Guides.
More cases will be added as I find more receipts/labels with applicable challenge levels.
These cases involved the calculations of these variables:
(A.) Initial price (Subtotal)
(B.) Tax rate
(C.) Tax
(D.) Total price
(E.) Discount
(F.) Percent discount
But, did you notice I did not do these variables?
(G.) Markup
(H.) Percent markup
It is for you to do if you wish.
(a.) Do at least 5 different cases.
At least one case should include a Discount and/or Percent Discount and/or a Markup and/or Percent
Markup.
(b.) Actual receipts should be used as best as you can.
However, if you cannot find an actual receipt or if you do not have the means to get an actual receipt:
Creativity and Technology Skills:
(i.) If you do not see any actual receipt/label involving markup and/or percent markup, use a suitable
software technology to
design the receipt/label.
(ii.) If you do not see any actual receipt/label involving discount and/or percent discount, use a
suitable software technology to
design the receipt/label.
(iii.) If you do not see any actual receipt/label involving the other cases, please contact me so I give
you the receipts.
(4.) English Language/Writing Skills: Using proper English Language grammar, write word problems
for each case.
Make sure you use words such as: percent, tax, tax rate, include, exclude, included, excluded, of,
and off among others.
(5.) Typing Skills: As a student, you most likely have free access to Microsoft Office suite of
apps.
(a.) Please use the computers in the Computer Lab of your school.
If you prefer to use your computer, please download the desktop apps of Microsoft Office on your
desktop/laptop (Windows and/or Mac only).
Do not use a chromebook.
Do not use a tablet/iPad.
Do not use a smartphone.
Do not use the web app/sharepoint access of Microsoft Office.
(Please contact the IT/Tech Support for assistance if you do not know how to download the desktop
app.)
In that regard, the project is to be typed using the desktop version/app of Microsoft Office Word
only.
(b.) The file name for the Microsoft Office Word project should be saved as:
firstName–lastName–project
Use only hyphens between your first name and your last name; and between your last name and the word,
project.
No spaces.
(c.) For all English terms (entire project): use Times New Roman; font size of 14; line spacing of 1.5
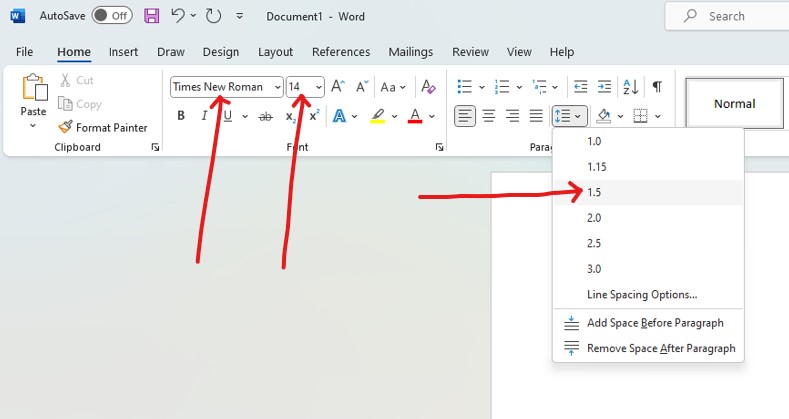
(d.) For all Math terms/work: symbols, variables, numbers, formulas, expressions, equations and
fractions among others,
the Math Equation Editor is required.
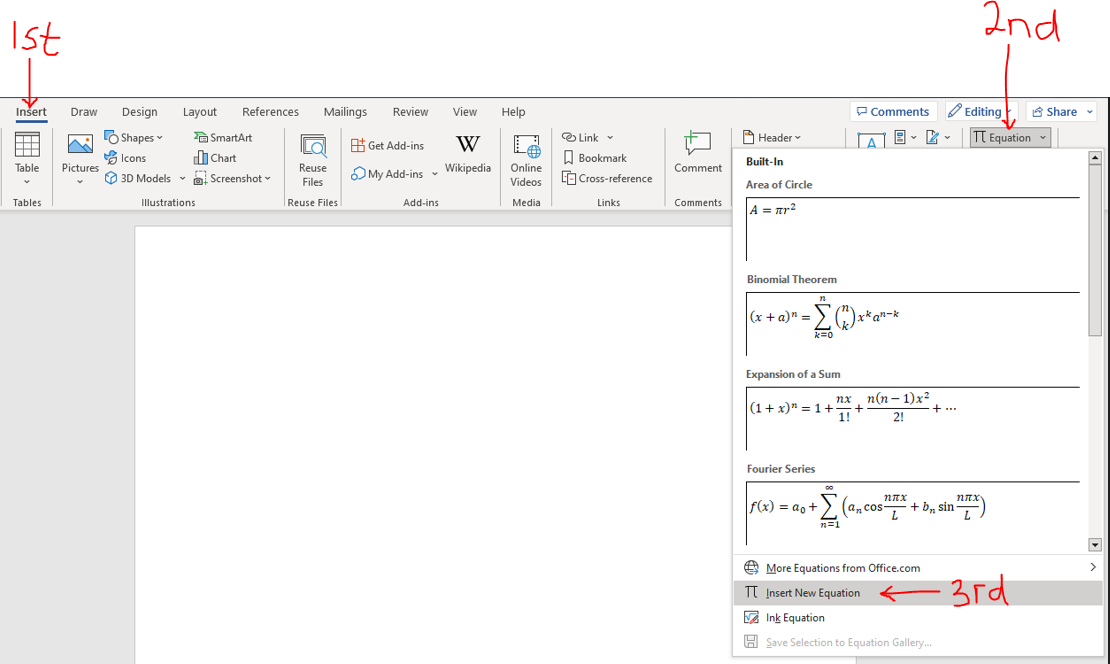
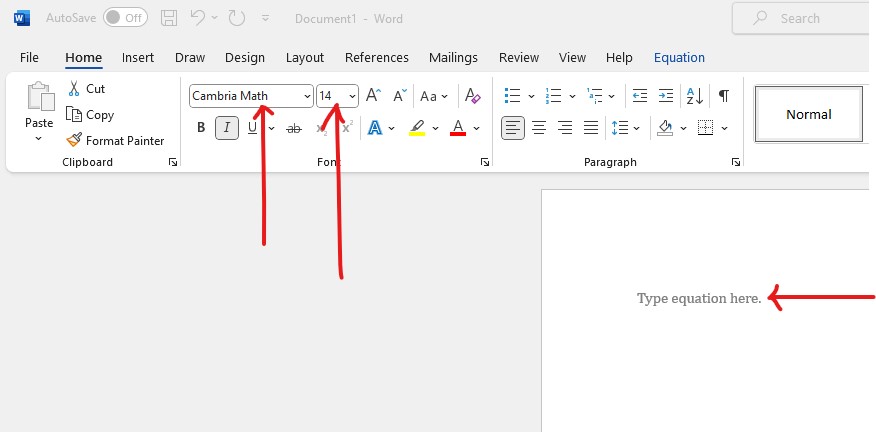
(i.) The font is set to Cambria Math by default (set it to that font if it is not); font size of 14, and
align accordingly (preferably left-aligned).
(ii.) To ensure appropriate spacing between your Math work, use a line spacing of 2.0.
Alternatively, you may use line spacing of 1.5 but insert a space after each equation as applicable.
Your work should be well-formatted, organized, well-spaced (not compact), and visually appealing.
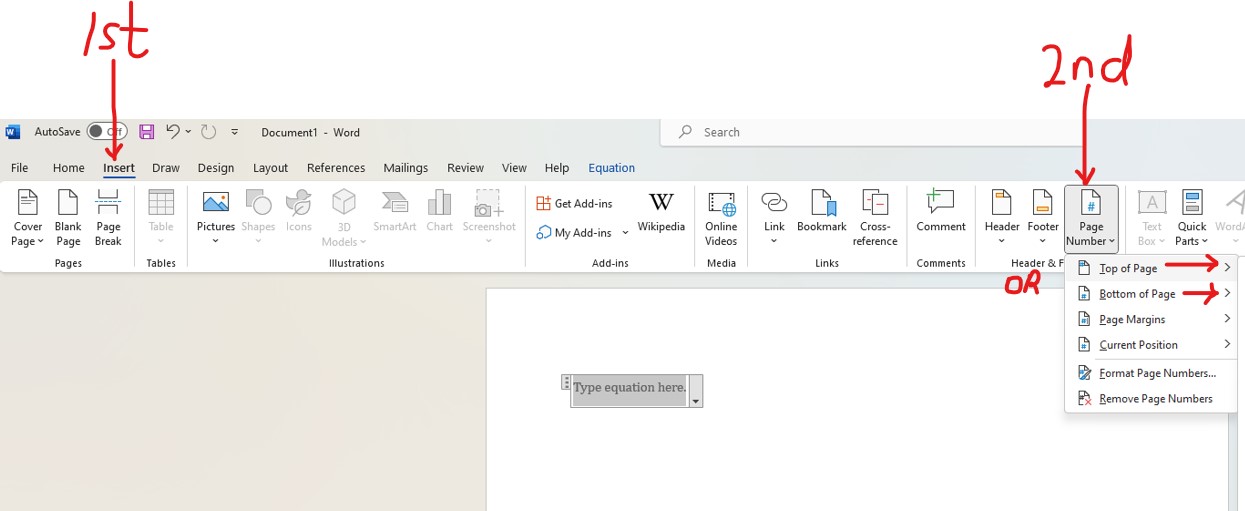
(e.) Include page numbers. You may include at the top of the pages or at the bottom of the pages but not
both.
(6.) Mathematical Skills/Reasoning: and Critical Thinking Skills:
(a.) Write any formula that you use.
(b.) Show all work.
(c.) Do not approximate intermediate calculations.
(d.) Approximate final answers accordingly.
(e.) The exact values must be shown prior to the approximate values.
(f.) Cases 3, 5, 6, 8: Notice the values I used in those cases. I used those values to get the values on
the receipts. In that same sense, you
may need to specify the values you used to get the values on the receipts.
(6.) Mr. C (SamDom For Peace) wants you to do this real-world project very well.
Hence, he highly recommends that you submit a draft so he can give you feedback.
(a.) First: (Required): Please submit clear images of the receipts in the Projects:
Receipts page in the Canvas course.
I shall review and respond.
(b.) Second: (Highly Recommended): When your receipts are approved, please submit your draft.
Draft projects are not graded because they are drafts. They are only for feedback.
If your professor gives you an opportunity to submit a draft, please use that opportunity.
Submitting drafts is highly recommended. Submitting drafts is not required.
It is highly recommended because I want to give you the opportunity to do your project very well and
make an excellent
grade in it.
Please turn in your draft in the Discussions page → Projects: Drafts forum in
the Canvas course
(if you would like your colleagues to read my comments and avoid any mistakes that you made).
You may also send it to me via email (if you do not want your colleagues to see my comments and learn
from the
comments).
I shall review and provide feedback.
Then, review my feedback and make changes as necessary.
Keep working with me until I give you the green light to turn in your actual project. This must
be done before
the final due date to turn in the actual project.
When everything is fine (after you make changes as applicable based on my feedback), please submit your
work in the appropriate area: Assignments page → Receipts Project in the Canvas
course.
Only the projects submitted in the appropriate place in the Canvas course are graded.
(7.) All work must be turned in by the final due date to receive credit.
Please note the due dates listed in the course syllabus for the submission of the draft and the actual
project.
In the course syllabus, we have the:
(a.) Initial due date for the Project Draft: Please turn in your draft.
(b.) Initial due date for the Project: If your draft is not ready for submission, keep working with me.
Make changes
based on my feedback and keep working with me.
If you prefer not to turn in a draft, please review all the resources provided for you and do your
project well and
submit.
(c.) Final due date for the Project Draft: This is necessary if you want a written feedback for your
draft.
After this date, written feedback would not be provided for your draft. However, verbal feedback would
still be provided
during Office Hours/Student Engagement Hours/Live Sessions.
(d.) Final due date for the Project: All work must be turned in by this date to receive credit.
After this date, no work may be accepted.
| Name: | Your name |
| Date: | The date |
| Instructor: | Samuel Chukwuemeka |
| Project: | Percent Application: Receipts |
| Objectives: |
Please write the objectives. Number them accordingly. |
| Cases: |
Please write each case. Number them accordingly. Insert the receipt for each case. Do the calculations for each case. |
| Citation: |
Indicate the type of citation format. Cite your source(s) accordingly. |
Student Project Samples
Sample 1: Ryan: Percent Application: Receipts ProjectSample 2: Velasquez: Percent Application: Receipts Project
Sample 3: Nieto: Percent Application: Receipts Project
The teacher should guide each student to the successful completion of the project.
Let students know you are willing to help.
References
Chukwuemeka, S.D (2024, March 10). Samuel Chukwuemeka Tutorials: Math, Science, and Technology.
Retrieved from https://quantitativereasoning.appspot.com/