The Mathematics of Finance using Texas Instruments Graphing Calculators

Welcome to VMATYC 2025 and to our Session

I greet you this day,
My name is Samuel Dominic Chukwuemeka (also known as SamDom For Peace).
I appreciate your attendance to this session.
If you do not mind, may we please take little time to introduce one another?
Name:
School/College/University:
Courses you teach:

Single Three-Year Software License Request Form
You may request for a complimentary three-year software license by completing the form at: https://ti-enews-education.ti.com/syllabus

You may use any of these TI calculators:
TI-83 Plus
TI-84 Plus series
TI-Nspire CX series
TI-89 Titanium
TI-73 Explorer

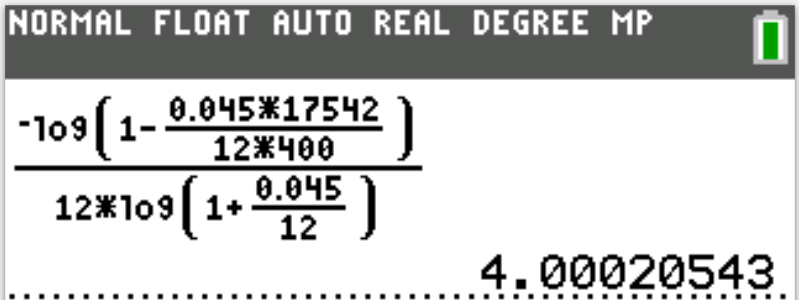
There are at least two approaches to using the TI-calculators for finance problems.
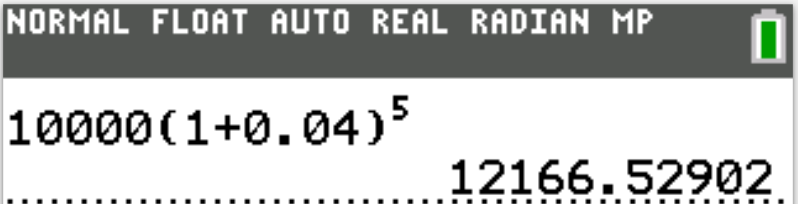
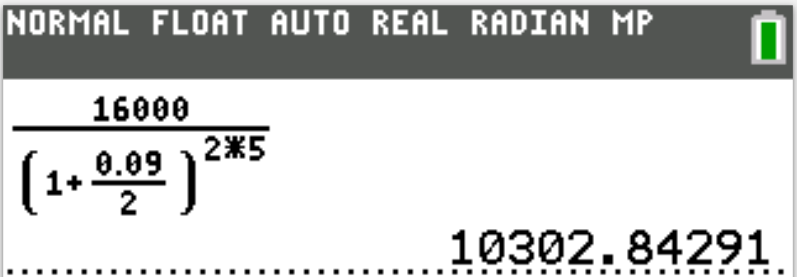
1st Approach: Direct Input of Substituted Values
(1.) Find the applicable Formula
(2.) Substitute the values directly in the formula.
(3.) Enter it directly in the calculator.
(Please see Show/Hide Answer for examples.)

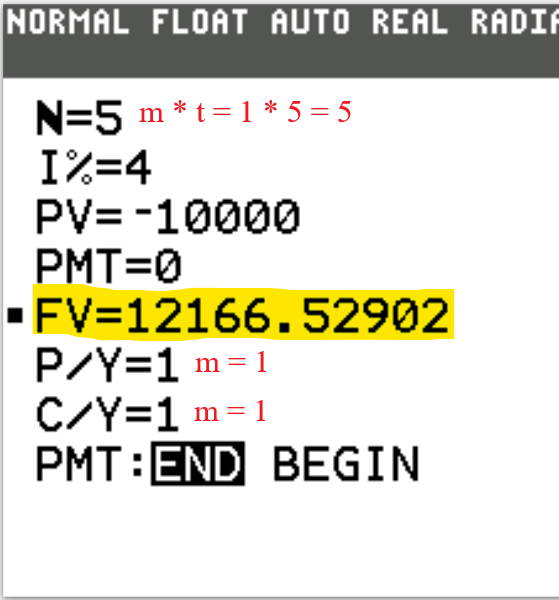
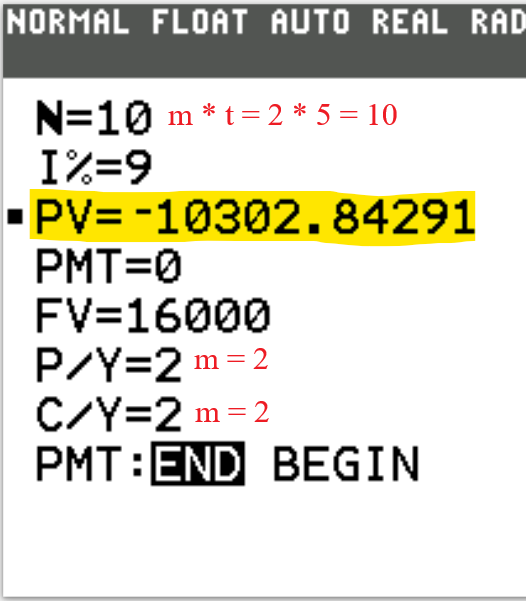
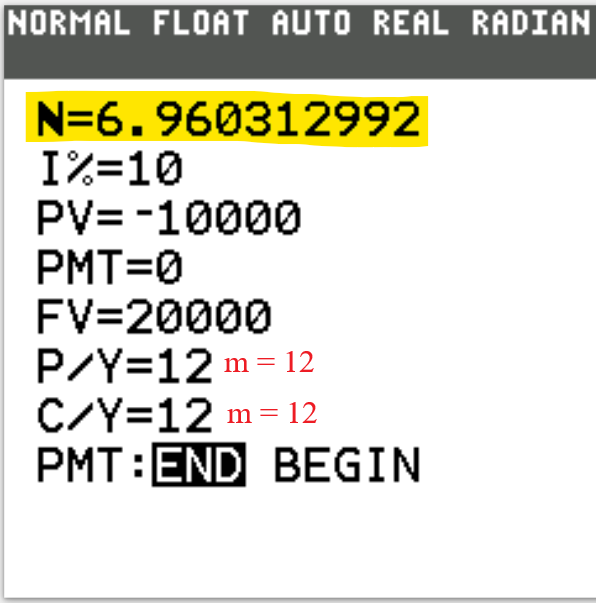
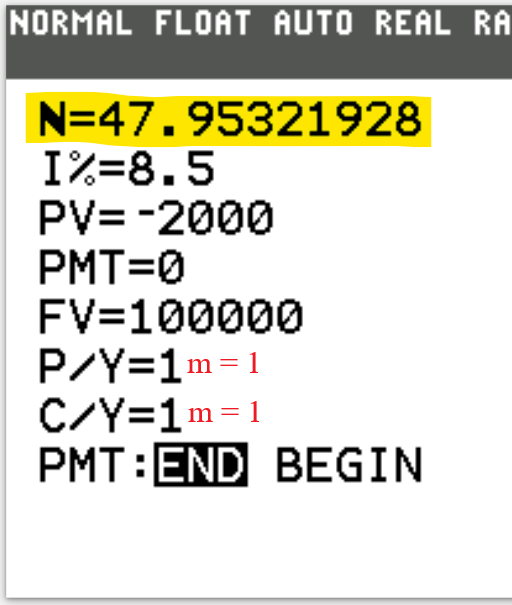
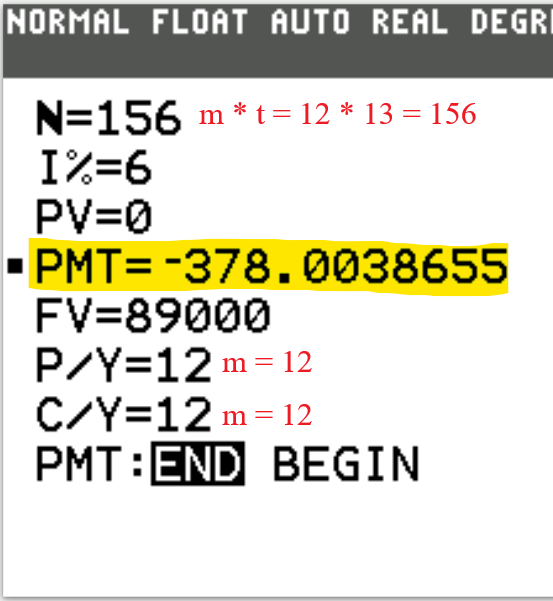
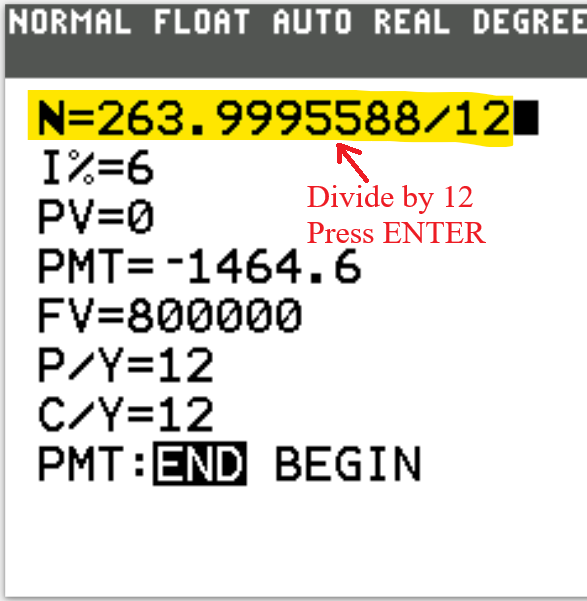
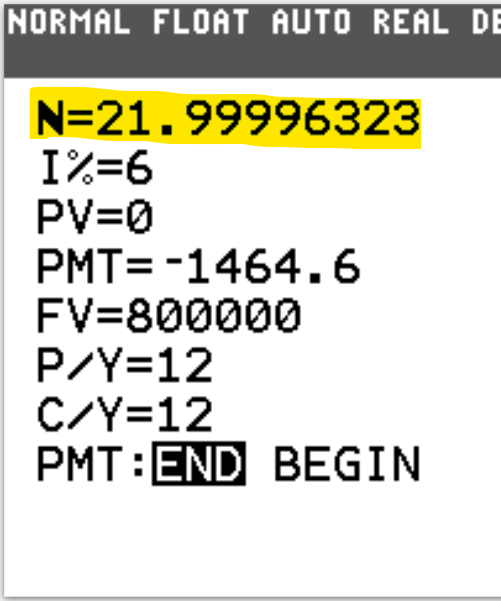
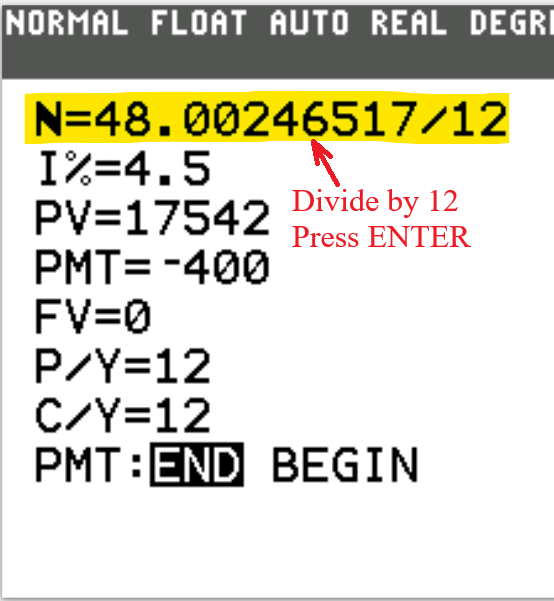
2nd Approach: Time Value of Money (TVM) Solver
The Finance app is required.
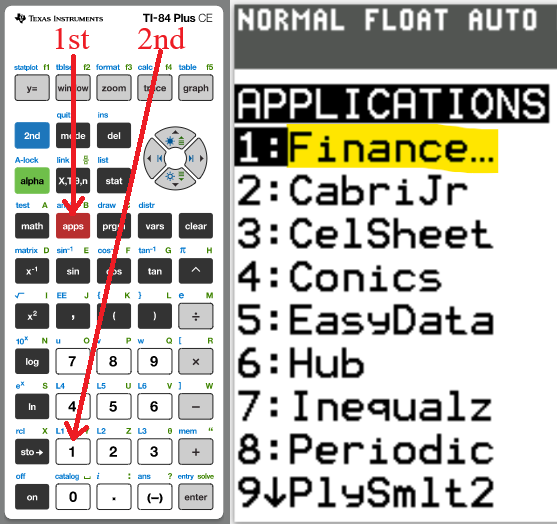
It can be assessed by pressing the APPS button, then pressing the 1: Finance app
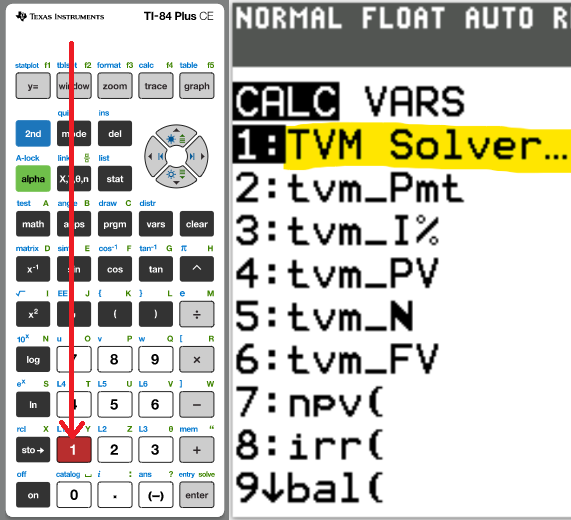
We begin with the TVM Solver (known as the Time Value of Money Solver) which is found as the first app under the CALC menu (CALC → 1: TVM Solver ...)

Finance App

For calculations involving:
Compound Interest
Continuous Compound Interest
Annuity
Amortization
We use the TVM-Solver

Calculations-1st

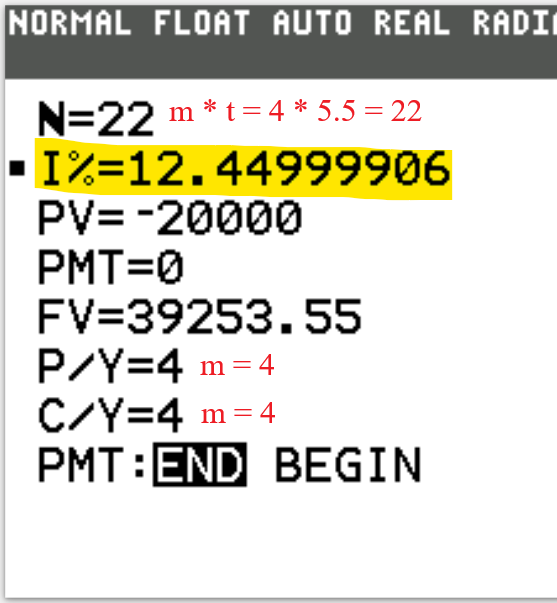
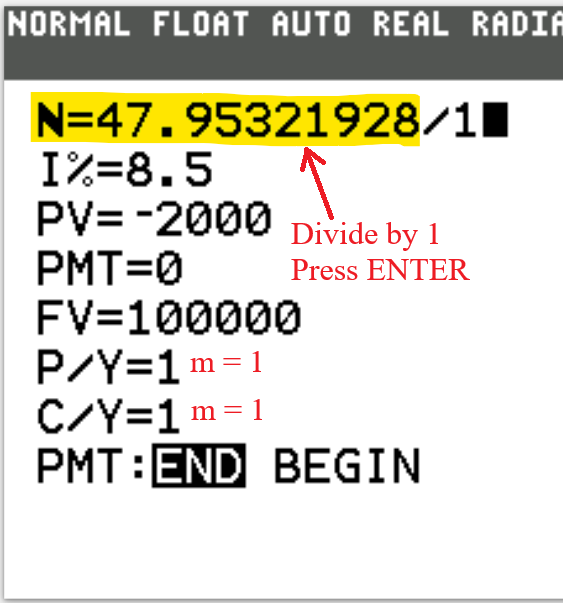
N is the total number of compounding periods (years).
$N = mt$
This is the product of the number of compounding periods per year and the time (in years).

I% is the interest rate.
If it is 3%, type 3. Do not include the %.

PV is the present value.
This is the Principal or Investment

PMT is the periodic payment.
This specifically applies to Annuity and Amortization.

FV is the future value.
This is the Amount.

P/Y is the number of payments per year.
C/Y is the number of compounding periods per year.
For Compound Interest and Continuous Compound Interest calculations, $P/Y = C/Y$

PMT:END:BEGIN Is the payment made at the end or at the beginning of the year?

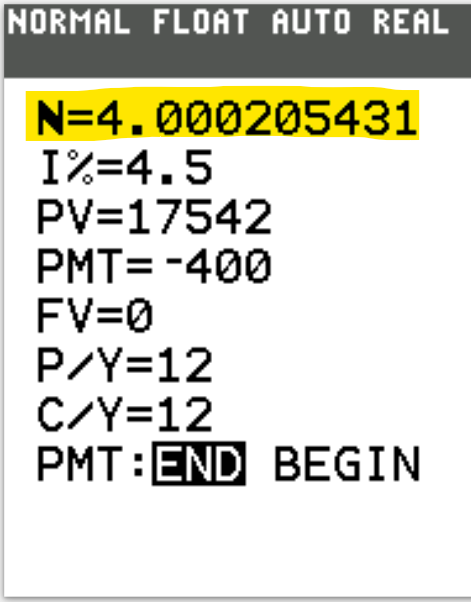
Notable Notes:
(1.) No field should be blank.
Put a value in every field.
If the field does not apply for the question, put a 0 in that field.
For the value that you would like to find, put 0 initially.

(2.) For any cash outflow, put a negative sign.
For any cash inflow, put a positive sign.

(3.) Indicate whether the payment is made at the END or at the BEGIN of a period.
When the black focus is on any of those options, move to the field that you want to calculate.

(4.) Clear the 0 that you put in initially in that field.
Press the ALPHA key
That takes us to the SOLVE menu which is above the ENTER key. So, press the ENTER key.
That gives the value of what you want to calculate.

For calculations involving:
Annual Percentage Rate
Annual Percentage Yield
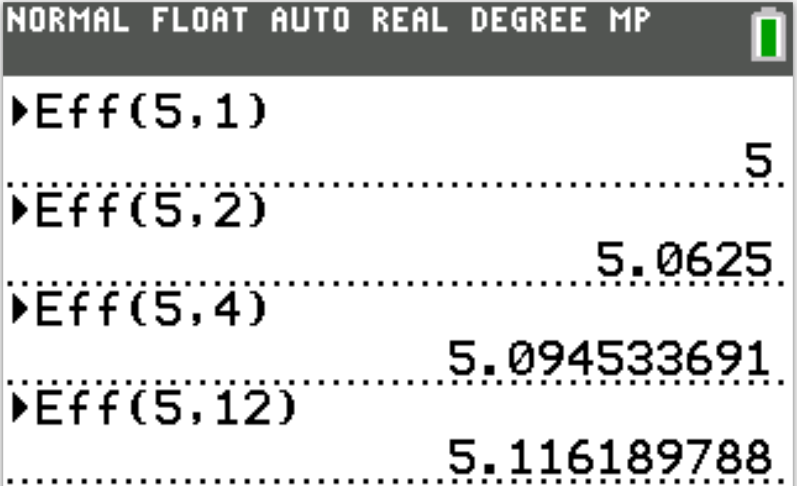
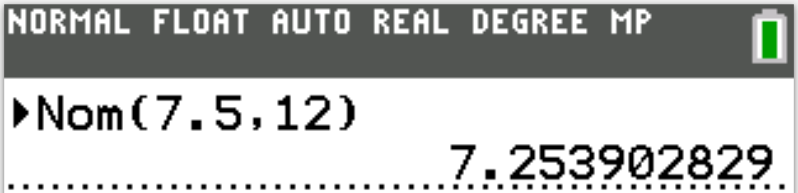
We use the Eff and Nom functions as applicable.
Use the codes as applicable:
Nom(APY, m)
Eff(APR, m)

Calculations-2nd

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome at anytime before, during or after the presentation.
Let us discuss the examples.
Thank you.

Objectives

The Mathematics of Finance is designed to:
(1.) Meet one of the learning objectives of the VCCS (Virginia Community College System) standards for:
MTH 130: Fundamentals of Reasoning
(Presents elementary concepts of algebra, linear graphing, financial literacy, descriptive statistics, and measurement & geometry. ).

MTH 154: Quantitative Reasoning
(Presents topics in proportional reasoning, modeling, financial literacy and validity studies (logic and set theory).).

MTH 165: Finite Math
(Presents topics in systems of equations, matrices, linear programming, mathematics of finance, counting theory, probability, and Markov Chains.).

(2.) Meet the QM (Quality Matters) and USDOE (United States Department of Education) requirements for distance education as regards the provision of RSI (Regular and Substantive Interaction).
Federal Register: Distance Education and Innovation
St. John's University: New Federal Requirements for Distance Education: Regular and Substantive Interaction (RSI)
Student – Content Interaction: Very high
Student – Student Interaction: High
Student – Faculty Interaction: High

(3.) Solve finance problems using technology: Texas Instruments (TI) calculators.

(4.) Solve finance problems using spreadsheets: Microsoft Excel and/or Google spreadsheets.

Skills Measured/Acquired
(1.) Use of prior knowledge
(2.) Critical Thinking
(3.) Interdisciplinary connections/applications
(4.) Technology
(5.) Active participation through direct questioning
(6.) Research

Symbols and Meanings

$Per\:\:annum$ OR $Per\:\:year$ OR $Annually$ OR $Yearly$ means for a year (per $1$ year)
$SI$ OR $I$ = Simple Interest or Dividend or Yield or Return ($)
$P$ = Principal or Present Value or Investment ($)
$r$ = Rate or Annual Interest Rate or Annual Percentage Rate (%)
$APR$ = Rate or Annual Percentage Rate (%)
$t$ = Time $(years)$
$A$ = Amount or Future Value ($)
$CI$ OR $I$ = Compound Interest or Yield or Dividend or Return($)
$m$ = Number of Compounding Periods Per Year
$n$ = Total Number of Compounding Periods $(years)$
$CCI$ = Continuous Compound Interest or Yield or Dividend or Return($)
$APY$ = Annual Percentage Yield or Effective Interest Rate or True Interest Rate (%)
$FV$ = Future Value ($)
$PMT$ = periodic payment ($)
$PMTs$ = total periodic payments ($)
$PV$ = Present Value of all payments ($)
$payoff$ = payoff amount for a mortgage
$k$ = number of remaining payments
$CFV$ = Combined Future Value ($)

Formulas

Simple Interest

$ (1.)\:\: SI = Prt \\[3ex] (2.)\:\: SI = A - P \\[3ex] (3.)\:\: P = \dfrac{SI}{rt} \\[5ex] (4.)\:\: t = \dfrac{SI}{Pr} \\[5ex] (5.)\:\: r = \dfrac{SI}{Pt} \\[5ex] (6.)\:\: A = P + SI \\[3ex] (7.)\:\: A = P(1 + rt) \\[3ex] (8.)\:\: P = \dfrac{A}{1 + rt} \\[5ex] (9.)\:\: t = \dfrac{A - P}{Pr} \\[5ex] (10.)\:\: r = \dfrac{A - P}{Pt} \\[5ex] (11.)\:\: SI = \dfrac{Art}{1 + rt} $

Compound Interest

$ (1.)\:\: A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[7ex] (2.)\:\: P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[10ex] (3.)\:\: r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[10ex] (4.)\:\: r = m\left(10^{\dfrac{\log\left(\dfrac{A}{P}\right)}{mt}} - 1\right) \\[10ex] (5.)\:\: t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] (6.)\:\: A = P + CI \\[3ex] (7.)\:\: CI = A - P $

Values of m

If Compounded:	m =
Annually	1 (1 time per year) Also means every twelve months
Semiannually	2 (2 times per year) Also means every six months
Quarterly	4 (4 times per year) Also means every three months
Monthly	12 (12 times per year) Also means every month
Weekly	52 (52 times per year)
Daily (Ordinary/Banker's Rule)	360 (360 times per year)
Daily (Exact)	365 (365 times per year)

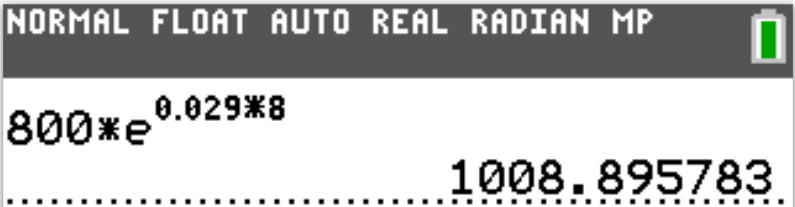
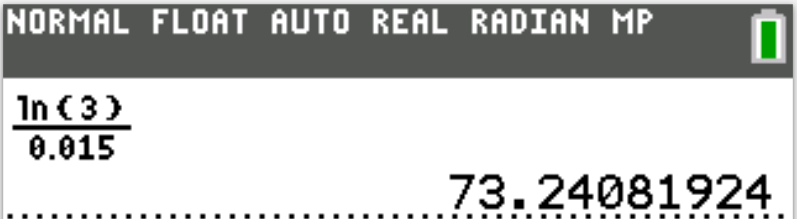
Continuous Compound Interest

$ (1.)\:\: A = Pe^{rt} \\[4ex] (2.)\:\: P = \dfrac{A}{e^{rt}} \\[7ex] (3.)\:\: t = \dfrac{\ln \left(\dfrac{A}{P}\right)}{r} \\[7ex] (4.)\:\: r = \dfrac{\ln \left(\dfrac{A}{P}\right)}{t} \\[7ex] (5.)\:\: A = P + CCI \\[3ex] (6.)\:\: CCI = A - P \\[3ex] $

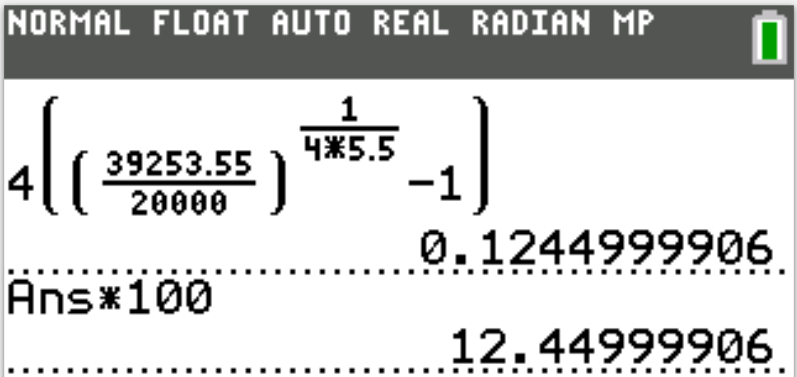
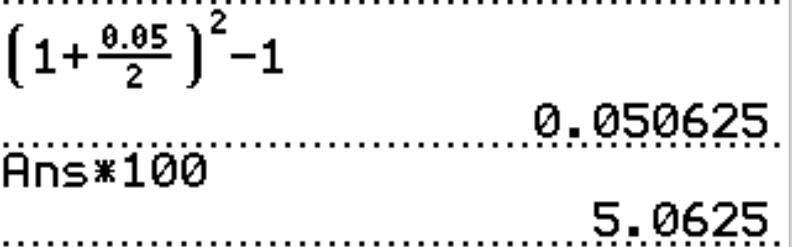
APY for Compound Interest

$ (1.)\:\: APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[7ex] (2.)\:\: r = m\left[(APY + 1)^{\dfrac{1}{m}} - 1\right] \\[7ex] (3.)\:\: r = m\left(\sqrt[m]{APY + 1} - 1\right) $

APY for Continuous Compound Interest

$ (1.)\:\: APY = e^r - 1 \\[4ex] (2.)\:\: r = \ln(APY + 1) $

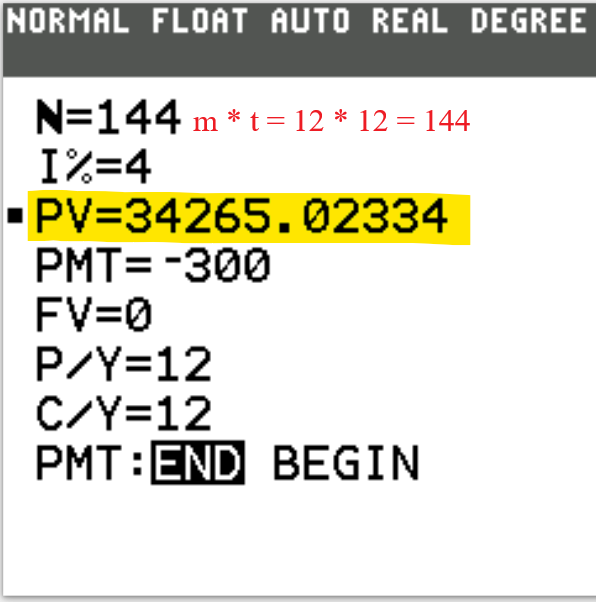
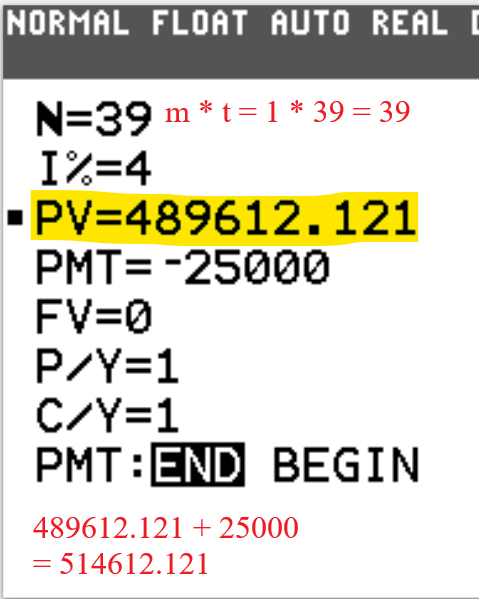
Future Value of Ordinary Annuity

$ (1.)\:\: FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] (2.)\;\; FV = PMT * \dfrac{\left[\left(1 + \dfrac{r}{m}\right)^{mt} - 1\right]}{\dfrac{r}{m}} \\[10ex] (3.)\:\: t = \dfrac{\log\left[\dfrac{r * FV}{m * PMT} + 1\right]}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] (4.)\:\: Total\:\:PMTs = PMT * m * t \\[3ex] (5.)\:\: CI = FV - Total\:\:PMTs \\[5ex] (6.)\:\: n = mt $

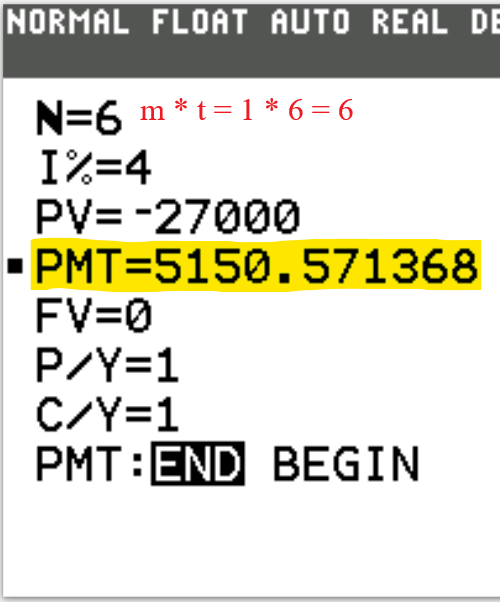
Sinking Fund

$ (1.)\:\: PMT = \dfrac{r * FV}{m * \left[\left(1 + \dfrac{r}{m}\right)^{mt} - 1\right]} \\[10ex] (2.)\:\: t = \dfrac{\log\left[\dfrac{r * FV}{m * PMT} + 1\right]}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] (3.)\:\: Total\:\:PMTs = PMT * m * t \\[3ex] (4.)\:\: CI = FV - Total\:\:PMTs \\[3ex] (5.)\:\: n = mt $

Present Value of Ordinary Annuity

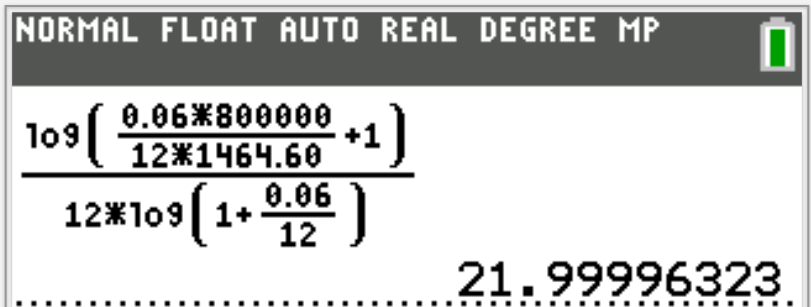
$ (1.)\:\: PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] (2.)\:\: t = -\dfrac{\log\left[1 - \dfrac{r * PV}{m * PMT}\right]}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] (3.)\:\: n = mt \\[3ex] (4.)\:\: Total\:\:PMTs = PMT * m * t \\[3ex] (5.)\:\: CI = Total\:\:PMTs - PV $

Amortization

$ (1.)\:\: PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] (2.)\:\: t = -\dfrac{\log\left[1 - \dfrac{r * PV}{m * PMT}\right]}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] (3.)\:\: n = mt \\[3ex] (4.)\:\: Payoff = PMT * n * \left[\dfrac{1 - \left(1 + \dfrac{r}{n}\right)^{-k}}{r}\right] \\[10ex] (5.)\:\: Total\:\:PMTs = PMT * m * t \\[3ex] (6.)\:\: CI = Total\:\:PMTs - PV \\[3ex] (7.)\:\: CI = PMT * m * t - PV \\[3ex] (8.)\:\: Number\:\:of\:\:payments = m * t \\[3ex] (9.)\:\: Down\:\:Payment = Given\:\:Rate * Purchase\:\:Price \\[3ex] (10.)\:\: Amount\:\:of\:\:Mortgage = Purchase\:\:Price - Down\:\:Payment \\[3ex] (11.)\:\: Payment\:\:for\:\:x\:\:points\:\:at\:closing = x\:\:as\:\:\% * Amount\:\:of\:\:Mortgage $

Formulas (PDF)

These formulas accommodate the TI-83 and the TI-84 models that do not have the fraction format: n/d: $\dfrac{numerator}{denominator}$
(Please see the formulas in red)

Compound Interest

(1.) ACT A formula used to compute the current value of a savings account is $A = P(1 + r)^n$, where A is the current value; P is the amount deposited; r is the rate of interest for 1 compounding period, expressed as a decimal; and n is the number of compounding periods.
Which of the following is closest to the value of a savings account after 5 years if $10,000 is deposited at 4% annual interest compounded yearly?

$ F.\;\; \$10,400 \\[3ex] G.\;\; \$12,167 \\[3ex] H.\;\; \$42,000 \\[3ex] J.\;\; \$52,000 \\[3ex] K.\;\; \$53,782 \\[3ex] $

$ P = \$10,000 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] n = 1(5) = 5\;years \\[3ex] A = P(1 + r)^n \\[3ex] A = 10000(1 + 0.04)^5 \\[3ex] A = 10000(1.04)^5 \\[3ex] A = 10000(1.216652902) \\[3ex] A = 12166.52902 \\[3ex] A \approx \$12,167 \\[3ex] $ Number 1

(2.) JAMB If the population of a town was 240000 in January 1998 and it increased by 2% each year, what would be the population of the town in January 2000?

$ A.\:\: 480,000 \\[3ex] B.\:\: 249,696 \\[3ex] C.\:\: 249,600 \\[3ex] D.\:\: 244,800 \\[3ex] $

We can solve this question in two ways: by using Quantitative Reasoning and the Compound Interest Formula
Use any way that is faster for you.

$ \underline{\text{First Approach: Quantitative Reasoning}} \\[3ex] \text{From January 1998 to January 2000} \implies 2000 - 1998 = 2\;years \\[3ex] From\:\:January,1998\:\:to\:\:January, 2000 \\[3ex] Population\:\:in\:\:1998 = 240000 \\[3ex] 2\%\:\:increase\:\:for\:\:1999 = \dfrac{2}{100} * 240000 = 2(2400) = 4800 \\[5ex] Population\:\:in\:\:1999 = 240000 + 4800 = 244800 \\[3ex] 2\%\:\:increase\:\:for\:\:2000 = \dfrac{2}{100} * 244800 = 2(2448) = 4896 \\[5ex] Population\:\:in\:\:2000 = 244800 + 4896 = 249696 \\[3ex] $ Ceteris paribus, the population of the town in January, $2000$ would be $249,696$ people

$ \underline{\text{Second Approach: Compound Interest Formula}} \\[3ex] \text{From January 1998 to January 2000} \implies 2000 - 1998 = 2\;years \\[3ex] P = 240000 \\[3ex] r = 2\% = \dfrac{2}{100} = 0.02 \\[5ex] t = 2\:years \\[3ex] m = 1 \\[3ex] A = ? \\[3ex] A = P\left(1 + \dfrac{r}{m}\right)^{mt} \\[5ex] A = 240000\left(1 + \dfrac{0.02}{1}\right)^{1(2)} \\[5ex] A = 240000(1 + 0.02)^2 \\[4ex] A = 240000(1.02)^2 \\[4ex] A = 240000(1.0404) \\[3ex] A = 249696 \\[3ex] $ Ceteris paribus, the population of the town in January, $2000$ would be $249,696$ people

Ask students their preferred method.
They should give reasons for their choices.

Number 2

(3.) Habakkuk wants to have $16000 in the future.
He intends to deposit some money in a company that pays 9% interest rate compounded semiannually.
How much should he deposit now to have that amount in 5 years time?

The question is asking us to calculate the principal.

$ A = \$16000 \\[3ex] r = 9\% = \dfrac{9}{100} = 0.09 \\[5ex] m = 2 \:\:(compounded\:\: semiannually) \\[3ex] t = 5 \\[3ex] P = \dfrac{A}{\left(1 + \dfrac{r}{m}\right)^{mt}} \\[7ex] P = \dfrac{16000}{\left(1 + \dfrac{0.09}{2}\right)^{2 * 5}} \\[7ex] P = \dfrac{16000}{(1 + 0.045)^{10}} \\[5ex] P = \dfrac{16000}{(1.045)^{10}} \\[5ex] P = \dfrac{16000}{1.552969422} \\[5ex] P = 10302.84291 \\[3ex] P = \$10302.84 \\[3ex] $ He should deposit $10302.84 now in order to earn $16000.00 in 5 years ceteris paribus

Number 3

(4.) How long will it take an investment of $10,000 to double if the investment earns interest at the rate of 10% per year compounded monthly?

$ P = \$10000 \\[3ex] A = double\:\:P = 2(10000) = \$20000 \\[3ex] r = 10\% = \dfrac{10}{100} = 0.1 \\[5ex] Compounded\:\:Monthly \implies m = 12 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] \dfrac{A}{P} = \dfrac{20000}{10000} = 2 \\[5ex] \dfrac{r}{m} = \dfrac{0.1}{12} = 0.0083333 \\[5ex] t = \dfrac{\log 2}{12 * \log(1 + 0.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * \log(1.0083333)} \\[5ex] t = \dfrac{0.301029995}{12 * 0.003604124} \\[5ex] t = \dfrac{0.301029995}{0.043249491} \\[5ex] t = 6.96031301 \\[3ex] t \approx 6.96 \\[3ex] $ It will take about 6.96 years for the investment of $10,000 to double at the rate of 10% per year compounded monthly.

Number 4

Given the answers in 7 decimal places, ask students to explain the reason for the different approximate answers.
Which answer is more precise?
To get the approximate answer given by the calculator and the Finance App, what needs to be done?

(5.) Five and a half years ago, Peter invested $20,000 which is worth $39,253.55 today if the rate is compounded quarterly.
What rate of interest is used?

$ t = 5\dfrac{1}{2}\: years = 5.5\: years \\[5ex] P = \$20000 \\[3ex] A = \$39253.55 \\[3ex] Compounded\:\:Quarterly \implies m = 4 \\[3ex] r = ? \\[3ex] r = m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] \\[7ex] mt = 4(5.5) = 22 \\[3ex] \dfrac{1}{mt} = \dfrac{1}{22} = 0.0454545455 \\[5ex] \dfrac{A}{P} = \dfrac{39253.55}{20000} = 1.9626775 \\[5ex] \left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} = 1.9626775^{0.0454545455} = 1.031125 \\[7ex] \left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1 = 1.031125 - 1 = 0.031125 \\[7ex] m\left[\left(\dfrac{A}{P}\right)^{\dfrac{1}{mt}} - 1\right] = 4(0.031125) = 0.1245 \\[7ex] 0.1245\:\:to\:\:\% = 0.1245(100) = 12.45\% \\[3ex] r = 12.45\% \\[3ex] $ The rate of interest is 12.45%

Number 5

(6.) $2000 is deposited in an account that pays an APR of 8.5% compounded annually.
How long will it take for the balance to reach $100,000?

$ r = 8.5\% = \dfrac{8.5}{100} = 0.085 \\[5ex] Compounded\:\:annually\rightarrow m = 1 \\[3ex] P = \$2000 \\[3ex] A = \$100000 \\[3ex] t = ? \\[3ex] t = \dfrac{\log\left(\dfrac{A}{P}\right)}{m\log\left(1 + \dfrac{r}{m}\right)} \\[7ex] t = \dfrac{\log\left(\dfrac{100000}{2000}\right)}{1 * \log\left(1 + \dfrac{0.085}{1}\right)} \\[7ex] t = \dfrac{\log (50)}{1 * \log(1 + 0.085)} \\[5ex] t = \dfrac{\log (50)}{1 * \log(1.085)} \\[5ex] t = \dfrac{\log (50)}{\log(1.085)} \\[5ex] t = 47.95321928 \\[3ex] t \approx 48\:years \\[3ex] $ Number 6

Continuous Compound Interest

(7.) Malachi invested a sum of $800 into an account that pays interest at the rate of 2.9% per year, compounded continuously.
How much money will be in the account after 8 years?
Round to the nearest hundredth as needed.

$ \underline{\text{Continuous Compound Interest}} \\[3ex] P = \$800 \\[3ex] t = 8\: years \\[3ex] r = 2.9\% = \dfrac{2.9}{100} = 0.029 \\[5ex] A = Pe^{rt} \\[5ex] A = 800 * e^{0.029 * 8} \\[5ex] = 800 * e^{0.232} \\[5ex] = 800 * 1.261119729 \\[2ex] = 1008.895783 \\[3ex] A \approx \$1008.90 \\[3ex] $ Number 7

(8.) The future value of Rita's investment in 7 years at 5% per annum compounded continuously is $7500.
What is the present value of her investment?

$ \underline{\text{Continuous Compound Interest}} \\[3ex] P = ? \\[3ex] t = 7\: years \\[3ex] r = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] A = \$7500 \\[3ex] P = \dfrac{A}{e^{rt}} \\[6ex] P = \dfrac{7500}{e^{0.05(7)}} \\[6ex] P = \dfrac{7500}{e^{0.35}} \\[6ex] P = \dfrac{7500}{1.419067549} \\[5ex] P = 5285.160673 \\[3ex] P \approx \$5285.16 \\[3ex] $ Number 8

(9.) Deborah invested $2000 at an interest rate, k compounded continuously.
The fund amounted to $2504.65 in 5 years.
Calculate the interest rate.

$ \underline{\text{Continuous Compound Interest}} \\[3ex] P = \$2000 \\[3ex] r = k \\[3ex] A = \$2504.65 \\[3ex] t = 5\:years \\[3ex] r = \dfrac{\ln \left({\dfrac{A}{P}}\right)}{t} \\[7ex] r = \dfrac{\ln \left({\dfrac{2504.65}{2000}}\right)}{5} \\[7ex] = \dfrac{\ln (1.252325)}{5} \\[5ex] = \dfrac{0.225001824}{5} \\[5ex] = 0.045000365 \\[3ex] to\:\:percent = 0.045000365(100) = 4.5000365 \\[3ex] r \approx 4.5\% \\[3ex] $ Number 9

(10.) If the population of SamDom For Peace City is growing at 1.5% compounded continuously, how long will it take the population to triple?

$ P = ? \\[3ex] A = 3P...triple \\[3ex] r = 1.5\% = \dfrac{1.5}{100} = 0.015 \\[5ex] t = ? \\[3ex] t = \dfrac{\ln \left(\dfrac{A}{P}\right)}{r} \\[7ex] t = \dfrac{\ln \left(\dfrac{3P}{P}\right)}{0.015} \\[7ex] = \dfrac{\ln 3}{0.015} \\[5ex] = \dfrac{1.09861229}{0.015} \\[5ex] = 73.2408192 \\[3ex] \approx 73.24\:years \\[3ex] $ Ceteris paribus, it will take approximately 73.24 years for the population of SamDom For Peace City to triple in size, if the population is growing at a rate of 1.5% compounded continuously.

Number 10

Annual Percentage Yield

(11.) Determine the effective rate of interest for a nominal rate of 5% per year compounded:
(a.) Annually
(b.) Semiannually
(c.) Quarterly
(d.) Monthly
(e.) Continuously

$ r = 5\% = \dfrac{5}{100} = 0.05 \\[5ex] (a.) \\[3ex] \underline{Annually} \\[3ex] Compounded\:\:annually \rightarrow m = 1 \\[3ex] APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[7ex] APY = \left(1 + \dfrac{0.05}{1}\right)^{1} - 1 \\[7ex] = \left(1 + 0.05\right)^{1} - 1 \\[5ex] = (1.05)^1 - 1 \\[3ex] = 1.05 - 1 \\[3ex] = 0.05 \\[3ex] to\:\:percent = 0.05(100) = 5\% \\[3ex] APY = 5\% \\[5ex] (b.) \\[3ex] \underline{Semiannually} \\[3ex] Compounded\:\:semiannually \rightarrow m = 2 \\[3ex] APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[7ex] APY = \left(1 + \dfrac{0.05}{2}\right)^{2} - 1 \\[7ex] = \left(1 + 0.025\right)^{2} - 1 \\[5ex] = (1.025)^2 - 1 \\[3ex] = 1.050625 - 1 \\[3ex] = 0.050625 \\[3ex] to\:\:percent = 0.050625(100) = 5.0625\% \\[3ex] APY = 5.0625\% \\[5ex] (c.) \\[3ex] \underline{Quarterly} \\[3ex] Compounded\:\:quarterly \rightarrow m = 4 \\[3ex] APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[7ex] APY = \left(1 + \dfrac{0.05}{4}\right)^{4} - 1 \\[7ex] = \left(1 + 0.0125\right)^{4} - 1 \\[5ex] = (1.0125)^4 - 1 \\[3ex] = 1.05094534 - 1 \\[3ex] = 0.05094534 \\[3ex] to\:\:percent = 0.05094534(100) = 5.094534\% \\[3ex] APY = 5.094534\% \\[5ex] (d.) \\[3ex] \underline{Monthly} \\[3ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] APY = \left(1 + \dfrac{r}{m}\right)^m - 1 \\[7ex] APY = \left(1 + \dfrac{0.05}{12}\right)^{12} - 1 \\[7ex] = \left(1 + 0.00416666667\right)^{12} - 1 \\[5ex] = (1.00416667)^{12} - 1 \\[3ex] = 1.05116194 - 1 \\[3ex] = 0.05116194 \\[3ex] to\:\:percent = 0.05116194(100) = 5.116194\% \\[3ex] APY = 5.116194\% \\[5ex] (e.) \\[3ex] \underline{Continuously} \\[3ex] APY = e^r - 1 \\[4ex] APY = e^{0.05} - 1 \\[4ex] = 1.0512711 - 1 \\[3ex] = 0.0512711 \\[3ex] to\:\:percent = 0.0512711(100) \\[3ex] APY = 5.12711\% \\[3ex] $ Number 11-1st

(12.) A loan company wants to offer a CD (Certificate of deposit) with a monthly company rate that has an APY of 7.5%.
What annual nominal rate compounded monthly should they use?

$ APY = 7.5\% = \dfrac{7.5}{100} = 0.075 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] r = m\left[(APY + 1)^{\dfrac{1}{m}} - 1\right] \\[7ex] r = 12 * \left[(0.075 + 1)^{\dfrac{1}{12}} - 1\right] \\[7ex] = 12 * \left[(1.075)^{\dfrac{1}{12}} - 1\right] \\[7ex] = 12 * \left[(1.075)^{0.0833333333} - 1\right] \\[5ex] = 12 * \left[1.00604492 - 1\right] \\[5ex] = 12 * 0.00604492 \\[3ex] = 0.07253904 \\[3ex] to\:\:percent = 0.07253904(10) = 7.253904 \\[3ex] r \approx 7.25\% \\[3ex] $ Number 12

Ordinary Annuity: Future Value and Sinking Fund

(13.) Calculate the future value of a $300 per week ordinary annuity at 4.5% per year compounded weekly for $8\dfrac{1}{2}$ years.
Assume 52 weeks in a year.

This is a case of the Future Value of Ordinary Annuity

$ \underline{Future\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$300 \\[3ex] r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] Compounded\:\:weekly \rightarrow m = 52 \\[3ex] t = 8\dfrac{1}{2}\:years = 8.5\:years \\[5ex] FV = ? \\[3ex] FV = m * PMT * \left[\dfrac{\left(1 + \dfrac{r}{m}\right)^{mt} - 1}{r}\right] \\[10ex] FV = 52 * 300 * \left[\dfrac{\left(1 + \dfrac{0.045}{52}\right)^{52 * 8.5} - 1}{0.045}\right] \\[10ex] = 15600 * \left[\dfrac{\left(1 + 0.000865384615\right)^{442} - 1}{0.045}\right] \\[10ex] = 15600 * \left[\dfrac{\left(1.000865384615\right)^{442} - 1}{0.045}\right] \\[7ex] = 15600 * \left[\dfrac{1.46570241 - 1}{0.045}\right] \\[5ex] = 15600 * \left[\dfrac{0.46570241}{0.045}\right] \\[5ex] = \dfrac{15600 * 0.46570241}{0.045} \\[5ex] = \dfrac{7264.9576}{0.045} \\[5ex] = 161443.502 \\[3ex] FV \approx \$161,443.50 \\[3ex] $ Ceteris paribus, the future value of a $300 per week ordinary annuity at 4.5% per year compounded weekly for $8\dfrac{1}{2}$ years is about $161,443.50

Number 13

(14.) Phoebe's goal is to create a college fund for her child.
She found a fund that offers an APR of 6%.
How much should she deposit monthly to accumulate $89000 in 13 years?

This is a case of Sinking Fund

$ r = 6\% = \dfrac{6}{100} = 0.06 \\[5ex] Monthly\;\;deposits \rightarrow Compounded\:\:monthly \rightarrow m = 12 \\[3ex] FV = \$89000 \\[3ex] t = 13\;years \\[3ex] PMT = \dfrac{r * FV}{m * \left[\left(1 + \dfrac{r}{m}\right)^{mt} - 1\right]} \\[9ex] = \dfrac{0.06 * 89000}{12 * \left[\left(1 + \dfrac{0.06}{12}\right)^{12 * 13} - 1\right]} \\[9ex] = \dfrac{5340}{12 * \left[(1 + 0.005)^{156} - 1\right]} \\[5ex] = \dfrac{5340}{12 * \left[(1.005)^{156} - 1\right]} \\[5ex] = \dfrac{5340}{12 * (2.177236639 - 1)} \\[5ex] = \dfrac{5340}{12 * 1.177236639} \\[5ex] = \dfrac{5340}{14.12683966} \\[5ex] = 378.0038655 \\[3ex] \approx \$378.00 \\[3ex] $ Phoebe should deposit about $378.00 in the college fund to have $89000 in 13 years ceteris paribus.

Number 14

(15.) At age 43, Augustine started saving for retirement.
He found an investment plan that pays an APR of 6%.
How long does he have to make a monthly deposit of $1464.60 to have $0.8 million in retirement?

This is a case of the Future Value of Ordinary Annuity

$ PMT = \$1464.60 \\[3ex] r = 6\% = \dfrac{6}{100} = 0.06 \\[5ex] Monthly\;\;payments \rightarrow Compounded\:\:monthly \rightarrow m = 12 \\[3ex] FV = \$0.8\;million = \$800,000 \\[3ex] t = ? \\[5ex] t = \dfrac{\log\left(\dfrac{r * FV}{m * PMT} + 1\right)}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] t = \dfrac{\log\left(\dfrac{0.06 * 800000}{12 * 1464.60} + 1\right)}{12 * \log\left(1 + \dfrac{0.06}{12}\right)} \\[10ex] t = \dfrac{\log\left(\dfrac{48000}{17575.2} + 1\right)}{12 * \log(1 + 0.005)} \\[10ex] t = \dfrac{\log(2.731121125 + 1)}{12 * \log(1.005)} \\[6ex] t = \dfrac{\log(3.731121125)}{12 * 0.0021660618} \\[5ex] t = \dfrac{0.571839348}{0.0259927411} \\[5ex] t = 21.99996321 \\[3ex] t \approx 22\;years \\[3ex] $ Number 15

Ordinary Annuity: Present Value and Amortization

(16.) Calculate the present value of a $300 per month ordinary annuity at 4% per year compounded monthly for 12 years.

This is a case of the Present Value of Ordinary Annuity

$ \underline{Present\:\:Value\:\:of\:\:Ordinary\:\:Annuity} \\[3ex] PMT = \$300 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] t = 12\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 12 * 300 * \left[\dfrac{1 - \left(1 + \dfrac{0.04}{12}\right)^{-1 * 12 * 12}}{0.04}\right] \\[10ex] = 3600 * \left[\dfrac{1 - \left(1 + 0.00333333333\right)^{-144}}{0.04}\right] \\[7ex] = 3600 * \left[\dfrac{1 - \left(1.00333333333\right)^{-144}}{0.04}\right] \\[7ex] = 3600 * \left[\dfrac{1 - 0.619277519}{0.04}\right] \\[5ex] = 3600 * \left[\dfrac{0.380722481}{0.04}\right] \\[5ex] = \dfrac{3600 * 0.380722481}{0.04} \\[5ex] = \dfrac{1370.60093}{0.04} \\[5ex] PV = 34265.0233 \\[3ex] PV \approx \$34,265.02 \\[3ex] $ Number 16

(17.) Felicity's parents set up a $27,000 trust fund for her.
She is to receive the money over a 6-year period in equal installments at the end of each year.
If the trust fund earns interest at the rate of 4% per year compounded annually, calculate the amount she will receive at the end of each year.

This is a case of Amortization

$ PV = \$27000 \\[3ex] t = 6\:years \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:annually \rightarrow m = 1 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{27000}{1} * \left[\dfrac{0.04}{1 - \left(1 + \dfrac{0.04}{1}\right)^{-1 * 1 * 6}}\right] \\[10ex] = 27000 * \left[\dfrac{0.04}{1 - \left(1 + 0.04\right)^{-6}}\right] \\[7ex] = 27000 * \left[\dfrac{0.04}{1 - \left(1.04\right)^{-6}}\right] \\[7ex] = 27000 * \left[\dfrac{0.04}{1 - 0.7903145257}\right] \\[5ex] = 27000 * \left[\dfrac{0.04}{0.2096854743}\right] \\[5ex] = \dfrac{27000 * 0.04}{0.2096854743} \\[5ex] = \dfrac{1080}{0.2096854743} \\[5ex] = 5150.571367 \\[3ex] PMT \approx \$5,150.57 \\[3ex] $ Number 17

(18.) Upright Capital, an investment firm purchased some acres of land for 5 million.
The firm made an initial down payment of 10% and obtained financing for the balance.
If the loan is to be amortized over 14 years at an interest rate of 5.1% per year compounded quarterly, find the required quarterly payment.

This is a case of Amortization

$ Purchase\:\:Price = \$5,000,000 \\[3ex] 10\%\:\:down\:\:payment = \dfrac{10}{100} * 5000000 = 25(24) = \$500000 \\[5ex] PV = \$5000000 - \$500000 = \$4500000 \\[3ex] t = 14\:years \\[3ex] r = 5.1\% = \dfrac{5.1}{100} = 0.051 \\[5ex] Compounded\:\:monthly \rightarrow m = 4 \\[3ex] PMT = ? \\[3ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}\right] \\[10ex] PMT = \dfrac{PV}{m} * \left[\dfrac{r}{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}\right] \\[10ex] PMT = \dfrac{4500000}{4} * \left[\dfrac{0.051}{1 - \left(1 + \dfrac{0.051}{4}\right)^{-1 * 4 * 14}}\right] \\[10ex] = 1125000 * \left[\dfrac{0.051}{1 - \left(1 + 0.012575\right)^{-56}}\right] \\[7ex] = 1125000 * \left[\dfrac{0.051}{1 - \left(1.01275\right)^{-56}}\right] \\[7ex] = 1125000 * \left[\dfrac{0.051}{1 - 0.4918966854}\right] \\[5ex] = 1125000 * \left[\dfrac{0.051}{0.5081033146}\right] \\[5ex] = \dfrac{1125000 * 0.051}{0.5081033146} \\[5ex] = \dfrac{57375}{0.5081033146} \\[5ex] = 112919.9483 \\[3ex] PMT \approx \$112,919.95 \\[3ex] $ Number 18

(19.) Grace Auto Sales is offering a financing package consisting of a 4.5% APR (Annual Percentage Rate) compounded monthly for their used vehicles.
Rebecca wants her monthly payments to be at most $400.
If the maximum amount that can be used to finance the purchase is $17542, how long will she need to make the monthly payments?

This is a case of Present Value of Ordinary Annuity

$ r = 4.5\% = \dfrac{4.5}{100} = 0.045 \\[5ex] Compounded\:\:monthly \rightarrow m = 12 \\[3ex] PMT = \$400 \\[3ex] PV = \$17542 \\[3ex] t = ? \\[5ex] t = -\dfrac{\log\left[1 - \dfrac{r * PV}{m * PMT}\right]}{m * \log\left(1 + \dfrac{r}{m}\right)} \\[10ex] t = -\dfrac{\log\left[1 - \dfrac{0.045 * 17542}{12 * 400}\right]}{12 * \log\left(1 + \dfrac{0.045}{12}\right)} \\[10ex] t = -\dfrac{\log\left[1 - \dfrac{789.39}{4800}\right]}{12 * \log\left(1 + 0.00375\right)} \\[8ex] t = -\dfrac{\log(1 - 0.16445625)}{12 * \log(1.00375)} \\[6ex] t = -\dfrac{\log(0.83554375)}{12 * 0.0016255583} \\[6ex] t = -\dfrac{-0.078030805}{0.0195066994} \\[5ex] t = 4.000205429 \\[3ex] t \approx 4\;years \\[3ex] $ She will need to make the monthly payments of $400 for at least 4 years (48-month term).

Number 19

(20.) The Phoenician Hotels has agreed to pay Sarah 40 installments of $25,000 per year in her lawsuit against them.
They intend to pay her $25,000 immediately and will make the other payments at the end of each of each year for the remaining years.
How much should they have in the bank to guarantee the payments, assuming that the balance on deposit with the bank earns interest at the rate of 4% per year compounded yearly?

40 installmental payments
Immediate payment of $\$25000$
Remaining payments = 40 − 1 = 39 payments = 39 years
This is a case of the Present Value of Ordinary Annuity

$ \underline{\text{Present Value of Ordinary Annuity}} \\[3ex] PMT = \$25000 \\[3ex] r = 4\% = \dfrac{4}{100} = 0.04 \\[5ex] Compounded\:\:yearly \rightarrow m = 1 \\[3ex] t = 39\:years \\[3ex] PV = ? \\[3ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-mt}}{r}\right] \\[10ex] PV = m * PMT * \left[\dfrac{1 - \left(1 + \dfrac{r}{m}\right)^{-1 * m * t}}{r}\right] \\[10ex] PV = 1 * 25000 * \left[\dfrac{1 - \left(1 + \dfrac{0.04}{1}\right)^{-1 * 1 * 39}}{0.04}\right] \\[10ex] = 25000 * \left[\dfrac{1 - \left(1 + 0.04\right)^{-39}}{0.04}\right] \\[7ex] = 25000 * \left[\dfrac{1 - \left(1.04\right)^{-39}}{0.04}\right] \\[7ex] = 25000 * \left[\dfrac{1 - 0.2166206064}{0.04}\right] \\[5ex] = 25000 * \left[\dfrac{0.7833793936}{0.04}\right] \\[5ex] = \dfrac{25000 * 0.7833793936}{0.04} \\[5ex] = \dfrac{19584.48484}{0.04} \\[5ex] PV = 489612.121 \\[3ex] PV \approx \$489,612.12 \\[3ex] $ To guarantee payments, The Phoenician Hotels should have:

$ 25000 + 489612.121 \\[3ex] = 514612.121 \\[3ex] \approx \$514,612.12 \\[3ex] $ Number 20

References

Chukwuemeka, S.D (2025, March 20). Samuel Chukwuemeka Tutorials: Math, Science, and Technology. Retrieved from https://quantitativereasoning.appspot.com/MathematicsFinance/financialMathematics.html

TI Products | Calculators and Technology | Texas Instruments. (n.d.). Education.ti.com. https://education.ti.com/en/products